Cronbach's Alpha with SPSS
Table of Contents
- Example Questionnaire Items and Data
- SPSS: Data Entry and Reliability Commands
- Analysis of Cronbach's Alpha Results
- Forming Composite Scores
1. Example Questionnaire Items and Data
To explain Cronbach's alpha, consider a research situation in which one wishes to assess the degree of internal consistency of scores from a set of indicators (questionnaire items). Assume the target group for this study is doctoral students in a course on questionnaire development. Two constructs are measured, task value for learning Cronbach's alpha and anxiety toward learning Cronbach's alpha.
The first variable of interest is Task Value and represents the degree to which the students believe the task at hand, in this case learning Cronbach's alpha, is valuable, important, or salient for whatever reason. Theorists studying Task Value suggests this construct may be composed for four domains: cost (effort required to complete the task of learning Cronbach's alpha), attainment value (level of importance one places on learning Cronbach's alpha), utility value (level at which Cronbach's alpha is judged to be relevant to current or future activities), and intrinsic value (level of interest and enjoyment one experiences from learning Cronbach's alpha).
To assess the level of Task Value that students place on learning Cronbach's alpha, the following questionnaire items are used:
Table 1
Task Value Items
| Not at all or only very minimal | To a small degree | To a moderate degree | To a considerable degree | To a great degree | |
| 1. To what degree do you find learning Cronbach's alpha interesting? | 1 | 2 | 3 | 4 | 5 |
| 2. What level or degree of importance do you place on learning Cronbach's alpha? | 1 | 2 | 3 | 4 | 5 |
| 3. How useful do you believe Cronbach's alpha to be to you? | 1 | 2 | 3 | 4 | 5 |
The second variable of interest is the level of anxiety students hold toward learning Cronbach's alpha. This variable will be called Anxiety and it reflects the level of worry and concern one may experience when thinking about learning Cronbach's alpha. Similar to test anxiety, Anxiety over learning Cronbach's alpha may consist of impairment in learning (losing focus, becoming confused), dread or worry (thoughts of failure or inadequacy), and negative physiological manifestations (nausea, sweating, difficulty breathing, headaches). To assess Anxiety, the following items are used:
Table 2
Anxiety Items
| Not at all or only very minimal | To a small degree | To a moderate degree | To a considerable degree | To a great degree | |
| 1. When you think about learning Cronbach's alpha, to what degree to you begin to feel physical symptoms of anxiety or nervousness? | 1 | 2 | 3 | 4 | 5 |
| 2. To what degree do you worry that learning Cronbach's alpha may be difficult for you? | 1 | 2 | 3 | 4 | 5 |
| 3. When thinking about learning mathematical and statistical concepts, such as Cronbach's alpha, to what degree do you lose your ability to concentrate? | 1 | 2 | 3 | 4 | 5 |
Note: The above six items are simply for instructional purposes only. They have not been reviewed or field tested.
Assume that these six items are administered to a group of 10 students, and their scores for each of the items are reported below in Table 3. The letters TV are added to items 1, 2, and 3 to help identify Task Value scores and the letter A is added to items 4, 5, and 6 to help identify Anxiety scores. Thus, TV1 represents Task Value item 1, and A5 represents Anxiety item 5.
Table 3
Scores on TV and A items from 10 students
| Student | TV1 | TV2 | TV3 | A4 | A5 | A6 |
| A | 4 | 5 | 4 | 1 | 1 | 1 |
| B | 4 | 4 | 5 | 2 | 3 | 4 |
| C | 1 | 3 | 4 | 3 | 3 | 4 |
| D | 2 | 1 | 2 | 2 | 2 | 1 |
| E | 3 | 4 | 3 | 1 | 1 | 1 |
| F | 1 | 1 | 1 | 4 | 4 | 4 |
| G | 5 | 5 | 4 | 5 | 4 | 3 |
| H | 4 | 4 | 4 | 4 | 4 | 5 |
| I | 2 | 3 | 4 | 1 | 2 | 1 |
| J | 1 | 2 | 1 | 5 | 5 | 5 |
From Table 3 note that the first student, student A, rated item TV1 a 4, rated item TV2 a 5, and item TV3 a 4. So this student judges the Task Value of Cronbach's alpha to be important, or, the average of this student's ratings on these three items falls between a rating of 4 "To a considerable degree" and a rating of 5 "To a great degree." However, in terms of Anxiety produced as a result of having to learn Cronbach's alpha, Student A provided a rating of 1 to all three items which suggests little to no anxiety for this student.
2. SPSS: Data Entry and Reliability Commands
With these data now consider how one calculates in SPSS Cronbach's alpha for both scales, Task Value and Anxiety. Below are step-by-step commands for calculating Cronbach's alpha in SPSS.
(a) Step 1
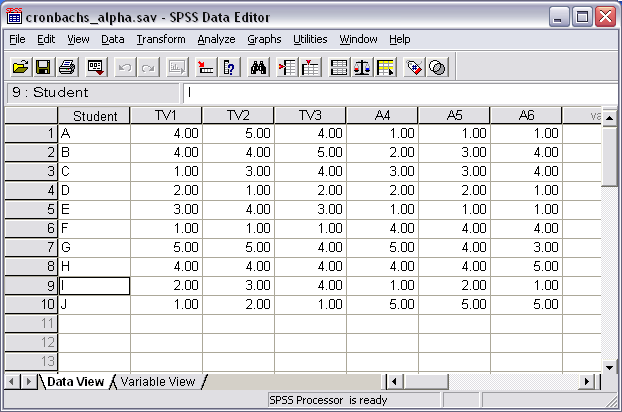
Enter the data into SPSS as shown above in Table 3. After data entry the SPSS screen should look something like Figure 1 below.
Figure 1
Data Entry of Task Value and Anxiety Items for each of
Ten Students
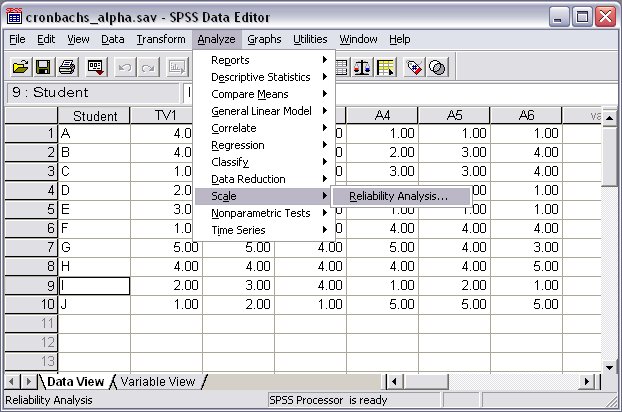
(b) Step 2
- Select "Analyze"
- Select "Scale"
- Select "Reliability Analysis"
Figure 2 shows how the current screen should appear.
Figure 2
Reliability Analysis Command
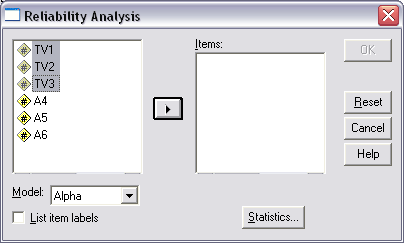
(c) Step 3
A pop-up window will appear for reliability analysis. In this window are two boxes, one to the left and one to the right. The left contains the variables, or items, entered in SPSS (TV1, TV2, etc.), the box to the right, which is labeled "Items," is where one moves those scale items for which Cronbach's alpha is desired. Note selected are the three Task Value items in Figure 3.
Figure 3
Reliability Analysis Pop-up Window
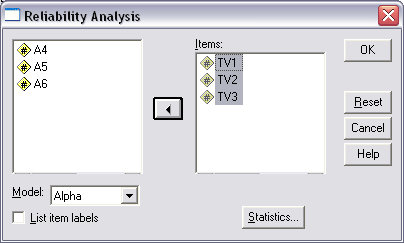
In Figure 4, note that the three Task Value items now appear in the box on the right; Cronbach's alpha will be calculated for the Task Value scores on these three items.
Important: If one also wanted to obtain Cronbach's alpha for the Anxiety items, one would have to re-run the analysis with only the Anxiety items appearing in the "Items:" box. To run Cronbach's alpha with both sets of items, Task Value and Anxiety, would be a mistake because those six items are not designed to measure the same construct and the alpha that would result would be uninterruptable.
Figure 4
Reliability Analysis Pop-up Window
(d) Step 4
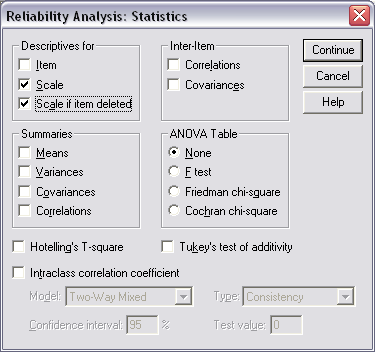
Select desired statistics for the analysis. Click on the "Statistics" button (see Figure 4). Once that button is selected, a pop-up window labeled "Statistics" will appear. This window is displayed in Figure 5 below. Note in Figure 5 the check mark next to "Scale" and "Scale if item deleted." Those boxes should be selected. After selecting those two options, then click on the "Continue" button to return to the "Reliability Analysis" pop-up window displayed above in Figure 4, then click on the "OK" button to run the analysis.
Figure 5
Statistical Options for Reliability Analysis
3. Analysis of Cronbach's Alpha Results
(a) Overall alpha
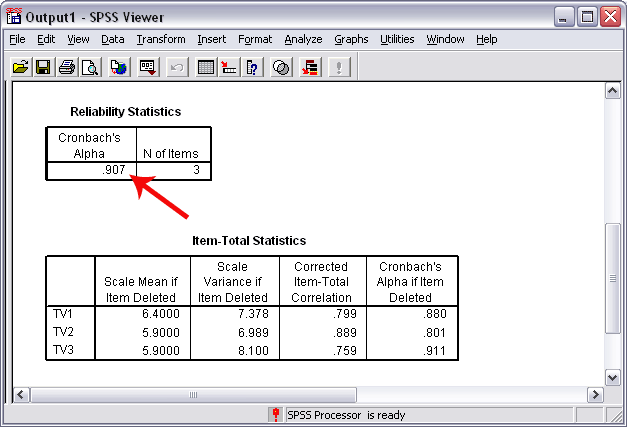
Figure 6 below displays some of the results obtained from SPSS. The red arrow points to the overall alpha for the three Task Value items. As the results in Figure 6 show, overall alpha is .907, which is very high and indicates strong internal consistency among the three Task Value items. Essentially this means that respondents who tended to select high scores for one item also tended to select high scores for the others; similarly, respondents who selected a low scores for one item tended to select low scores for the other Task Value items. Thus, knowing the score for one Task Value item would enable one to predict with some accuracy the possible scores for the other two Task Value items. Had alpha been low, this ability to predict scores from one item would not be possible.
Figure 6
Statistical Results for Reliability Analysis (overall
alpha highlighted)
(b) Corrected Item-Total Correlation
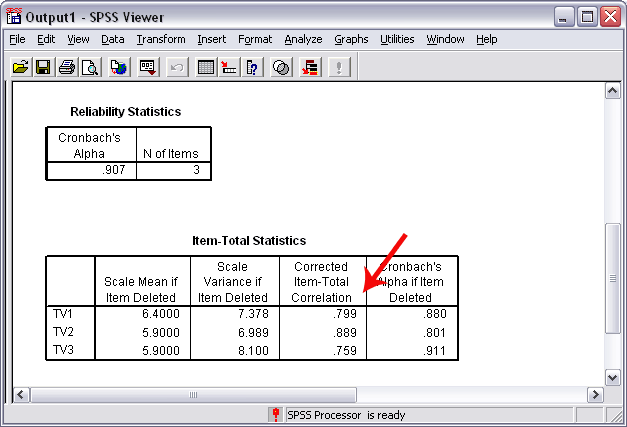
Figure 7 below highlights the column containing the "Corrected Item-Total Correlation" for each of the items. This column displays the correlation between a given Task Value item and the sum score of the other two items. For example, the correlation between Task Value item 1 and the sum of items 2 and 3 (i.e., item 2 + item 3) is r = .799. This means is that there is a strong, positive correlation between the scores on the one item (item 1) and the combined score of the other two (items 2 and 3). This correlation enables one to determine the level of internal consistency of one item's scores with the composite scores from all other items designed to measure the same construct. If this correlation is weak (de Vaus suggests anything less than .30 is a weak correlation for item-analysis purposes [de Vaus (2004), Suveys in Social Research, Routledge, p. 184]), then that item should be removed and not used to form a composite score for the variable in question. For example, if the correlation between scores for item 1 and the combined scores of items 2 and 3 was low, say r = .15, then when a composite score, or overall score, of Task Value is created, one should we create the composite using only items 2 and 3 and ignore scores from item 1 because it was not internally consistent with the other items. This decision to remove one item, however, should not be based exclusively upon results of the item analysis--theory and practice should also be a guide as to which items should be retained or removed.
Figure 7
Statistical Results for Reliability Analysis
(Corrected Item-Total Correlation)
(c) Cronbach's Alpha if item Deleted
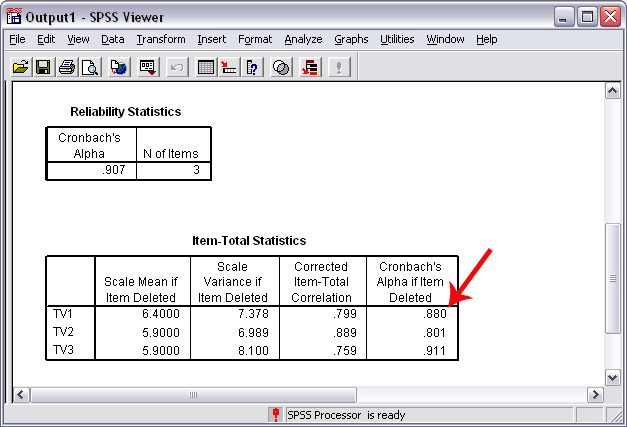
Figure 8 displays the Cronbach's alpha that would result if a given item were deleted. Like the item-total correlation presented above in (b), this column of information is valuable for determining which items from among a set of items contributes to the total alpha. The value presented in this column represents the alpha value if the given item were not included. For example, for Task Value item 1, the Cronbach's alpha if item 1 were deleted would drop from the overall total of .907 to .880. Since alpha would drop with the removal of TV1, this item appears to be useful and contributes to the overall consistency of Task Value. Item 3, however may be less valuable. Cronbach's alpha would increase from .907 to .911 if item 3 were deleted or not used for computing an overall Task Value score. So should this item be removed and should the overall Task Value composite be created only from items 1 and 2? In this case the answer is no, one should instead retain all three items. Why? Note first that alpha does not increase by a large degree from deleting item 3. Second, note that item 3 still correlates very well with the composite score from items 1 and 2 (the item-total correlation for item 3 is .759). Since deletion of item 3 results in little change, and since item 3 correlates well with the composite of items 1 and 2, there is no statistical reason to drop item 3. In this case theory and practice should be a guide as to whether to remove or retain item 3. If the wording of item 3 is theoretically important to measure Task Value, then item 3 should remain in forming the composite score for Task Value.
Figure 8
Statistical Results for Reliability Analysis (Cronbach's
Alpha if item Deleted)
4. Forming Composite Scores
When analysis of the contribution of each item is complete --- item analyses are run and re-run as needed to consider what happens when items are removed --- then it is time to move toward creating the composite score for the construct in question. For example, from the analysis above it appears that all three items designed to measure Task Value work well and contribute to overall reliability of Task Value, so all will be retained. One must now create a composite score to arrive at a measure of Task Value for each study participant. Below, in Table 4, are scores for the three Task Value items for each student. Two new columns were added. The first shows how to create a total score for Task Value, the second a mean score for Task Value.
Computing a composite score from the mean provides two advantages. First, the composite score calculated from the mean will retain the original scale of measurement, which, in this example, ranges from 1 to 5. Since mean scores are constrained within the original metric, they are therefore easier to interpret, that is, the mean score can be understood within the original scale. So, for instance, student A's mean score is 4.33 which indicates that student's scores were in the upper end of the range of responses whereas Student D's responses average toward the lower end of the results (close to 1). A second advantage with the mean is that it provides correctly scaled composite score when missing data occurs as long as the mean is divided by the number of contributing items and not the total number of items. SPSS's Mean function and Excel's Average function make this adjustment automatically.
Composite scores are important because they reflect the total set of responses to the items designed to measure Task Value, in this example. Analysis based upon scores from single items would likely be less reliable and valid. Given this, any additional analyses to answer research questions about Task Value would focus on the composite score. So, for instance, if one were interested in the difference in Task Value between males and females, one would perform the ANOVA or t-test using the mean Task Value score for each student (or, if preferred, the summed score for Task Value). Similarly, if one wished to learn whether Task Value correlates with Anxiety, one would calculate Pearson's r between the mean scores of Task Value and and the mean scores for Anxiety---Pearson's r would be calculated based upon the two composite variables, one for Task Value and one for Anxiety.
Table 4
Composite Score for Task Value
| Student | TV1 | TV2 | TV3 | Option 1---Total Score for Task Value | Option 2 --- Mean Score for Task Value |
| A | 4 | 5 | 4 | 4+5+4 = 13 | 4+5+4 = 13/3 = 4.33 |
| B | 4 | 4 | 5 | 4+4+5 = 13 | 4+4+5 = 13/3 = 4.33 |
| C | 1 | 3 | 4 | 1+3+4 = 8 | 1+3+4 = 8/3 = 2.66 |
| D | 2 | 1 | 2 | 2+1+2 = 5 | 2+1+2 = 5/3 = 1.66 |
| E | 3 | 4 | 3 | etc. | etc. |
| F | 1 | 1 | 1 | ||
| G | 5 | 5 | 4 | ||
| H | 4 | 4 | 4 | ||
| I | 2 | 3 | 4 | ||
| J | 1 | 2 | 1 |
Copyright 2010, College of Education, Georgia Southern University
Created by Bryan W. Griffin
Thursday, August 18, 2011
18 August, 2011 11:55 AM